Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 91, pp. 1-11.
Existence of three solutions for a Kirchhoff-type
boundary-value problem
Shapour Heidarkhani, Ghasem Alizadeh Afrouzi, Donal O'Regan
Abstract:
In this note, we establish the existence of two intervals of
positive real parameters
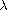 for which the boundary-value
problem of Kirchhoff-type
for which the boundary-value
problem of Kirchhoff-type
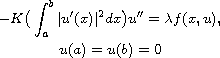
admits three weak solutions whose norms are
uniformly bounded with respect to
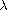 belonging to one of the
two intervals. Our main tool is a three critical point theorem by
Bonanno.
belonging to one of the
two intervals. Our main tool is a three critical point theorem by
Bonanno.
Submitted April 26, 2011. Published July 6, 2011.
Math Subject Classifications: 35J20, 35J25, 35J60.
Key Words: Kirchhoff-type problem; multiple solutions; critical point.
Show me the PDF file (241 KB),
TEX file, and other files for this article.
 |
Shapour Heidarkhani
Department of Mathematics
Faculty of Sciences, Razi University
67149 Kermanshah, Iran
email: s.heidarkhani@razi.ac.ir
|
|---|
 |
Ghasem Alizadeh Afrouzi
Department of Mathematics, Faculty of Basic Sciences
University of Mazandaran, 47416-1467 Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Donal O'Regan
Department of Mathematics
National University of Ireland
Galway, Ireland
email: donal.oregan@nuigalway.ie
|
|---|
Return to the EJDE web page
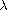 for which the boundary-value
problem of Kirchhoff-type
for which the boundary-value
problem of Kirchhoff-type
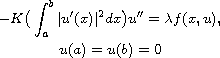
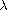 belonging to one of the
two intervals. Our main tool is a three critical point theorem by
Bonanno.
belonging to one of the
two intervals. Our main tool is a three critical point theorem by
Bonanno.


