Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 88, pp. 1-12.
Asymptotic behavior of ground state solutions for sublinear and
singular nonlinear Dirichlet problems
Rym Chemmam, Abdelwaheb Dhifli, Habib Maagli
Abstract:
In this article, we are concerned with the asymptotic behavior
of the classical solution to the semilinear boundary-value
problem
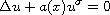
in
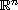 ,
,
 ,
,
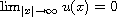 ,
where
,
where
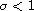 .
The special feature is to consider the
function
.
The special feature is to consider the
function
 in
in
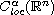 ,
,
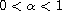 ,
such that there exists
,
such that there exists
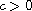 satisfying
satisfying
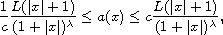
where
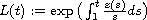 ,
with
,
with
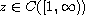 such that
such that
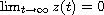 .
The comparable asymptotic rate of
.
The comparable asymptotic rate of
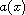 determines the asymptotic
behavior of the solution.
determines the asymptotic
behavior of the solution.
Submitted April 13, 2011. Published July 5, 2011.
Math Subject Classifications: 31B05, 31C35, 34B27, 60J50.
Key Words: Asymptotic behavior; Dirichlet problem; ground sate solution;
singular equations; sublinear equations.
Show me the PDF file (266 KB),
TEX file, and other files for this article.
 |
Rym Chemmam
Département de Mathématiques,
Faculté des Sciences de Tunis
Université Tunis El Manar, Campus universitaire
2092 Tunis, Tunisia
email: Rym.Chemmam@fst.rnu.tn
|
|---|
 |
Abdelwaheb Dhifli
Département de Mathématiques,
Faculté des Sciences de Tunis
Université Tunis El Manar, Campus universitaire
2092 Tunis, Tunisia
email: dhifli_waheb@yahoo.fr
|
|---|
 |
Habib Mâagli
Département de Mathématiques,
Faculté des Sciences de Tunis
Université Tunis El Manar, Campus universitaire
2092 Tunis, Tunisia
email: habib.maagli@fst.rnu.tn
|
|---|
Return to the EJDE web page
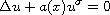
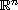 ,
,
 ,
,
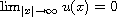 ,
where
,
where
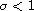 .
The special feature is to consider the
function
.
The special feature is to consider the
function
 in
in
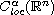 ,
,
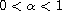 ,
such that there exists
,
such that there exists
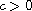 satisfying
satisfying
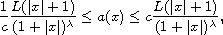
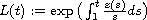 ,
with
,
with
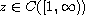 such that
such that
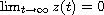 .
The comparable asymptotic rate of
.
The comparable asymptotic rate of
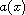 determines the asymptotic
behavior of the solution.
determines the asymptotic
behavior of the solution.


