Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 81, pp. 1-13.
Existence of continuous positive solutions for some
nonlinear polyharmonic systems outside the unit ball
Sameh Turki
Abstract:
We study the existence of continuous positive solutions of the
m-polyharmonic nonlinear elliptic system
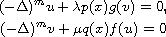
in the complement of the unit closed ball in
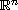 (n>2m and
(n>2m and
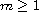 ).
Here the constants
).
Here the constants
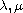 are
nonnegative, the functions f,g are nonnegative, continuous and
monotone. We prove two existence results for the above system
subject to some boundary conditions, where the nonnegative
functions p,q satisfy some appropriate conditions related
to a Kato class of functions.
are
nonnegative, the functions f,g are nonnegative, continuous and
monotone. We prove two existence results for the above system
subject to some boundary conditions, where the nonnegative
functions p,q satisfy some appropriate conditions related
to a Kato class of functions.
Submitted May 23, 2011. Published June 21, 2011.
Math Subject Classifications: 34B27, 35J40.
Key Words: Polyharmonic elliptic system; Positive solutions;
Green function; polyharmonic Kato class.
Show me the PDF file (255 KB),
TEX file, and other files for this article.
 |
Sameh Turki
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: sameh.turki@ipein.rnu.tn
|
|---|
Return to the EJDE web page
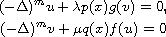
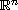 (n>2m and
(n>2m and
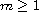 ).
Here the constants
).
Here the constants
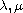 are
nonnegative, the functions f,g are nonnegative, continuous and
monotone. We prove two existence results for the above system
subject to some boundary conditions, where the nonnegative
functions p,q satisfy some appropriate conditions related
to a Kato class of functions.
are
nonnegative, the functions f,g are nonnegative, continuous and
monotone. We prove two existence results for the above system
subject to some boundary conditions, where the nonnegative
functions p,q satisfy some appropriate conditions related
to a Kato class of functions.
