Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 79, pp. 1-9.
Existence and asymptotic behaviour of positive solutions for semilinear
elliptic systems in the Euclidean plane
Abdeljabbar Ghanmi, Faten Toumi
Abstract:
We study the semilinear elliptic system
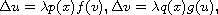
in an unbounded domain D in
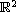 with compact
boundary subject to some Dirichlet conditions. We give existence
results according to the monotonicity of the nonnegative
continuous functions f and g. The potentials p and q are
nonnegative and required to satisfy some hypotheses related on a
Kato class.
with compact
boundary subject to some Dirichlet conditions. We give existence
results according to the monotonicity of the nonnegative
continuous functions f and g. The potentials p and q are
nonnegative and required to satisfy some hypotheses related on a
Kato class.
Submitted March 31, 2011. Published June 20, 2011.
Math Subject Classifications: 34B27, 35J45, 45M20.
Key Words: Green function; semilinear elliptic systems;
positive solution.
Show me the PDF file (230 KB),
TEX file, and other files for this article.
 |
Abdeljabbar Ghanmi
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: ghanmisl@yahoo.fr
|
|---|
 |
Faten Toumi
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: faten.toumi@fsb.rnu.tn
|
|---|
Return to the EJDE web page
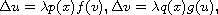
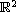 with compact
boundary subject to some Dirichlet conditions. We give existence
results according to the monotonicity of the nonnegative
continuous functions f and g. The potentials p and q are
nonnegative and required to satisfy some hypotheses related on a
Kato class.
with compact
boundary subject to some Dirichlet conditions. We give existence
results according to the monotonicity of the nonnegative
continuous functions f and g. The potentials p and q are
nonnegative and required to satisfy some hypotheses related on a
Kato class.

