Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 75, pp. 1-10.
Three positive solutions for m-point boundary-value problems
with one-dimensional p-Laplacian
Donglong Bai, Hanying Feng
Abstract:
In this article, we study the multipoint boundary value
problem for the one-dimensional p-Laplacian
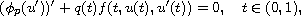
subject to the boundary conditions
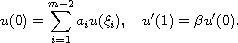
Using a fixed point theorem due to Avery and Peterson, we provide
sufficient conditions for the existence of at least three positive
solutions to the above boundary value problem. The interesting point
is that the nonlinear term f involves the first
derivative of the unknown function.
Submitted April 5, 2011. Published June 16, 2011.
Math Subject Classifications: 34B10, 34B15, 34B18.
Key Words: Multipoint boundary value problem; positive solution;
Avery-Peterson fixed point theorem; one-dimensional p-Laplacian.
Show me the PDF file (223 KB),
TEX file, and other files for this article.
 |
Donglong Bai
Department of Mathematics
Shijiazhuang Mechanical Engineering College
Shijiazhuang 050003, Hebei, China
email: baidonglong@yeal.net
|
|---|
 |
Hanying Feng
Department of Mathematics
Shijiazhuang Mechanical Engineering College
Shijiazhuang 050003, Hebei, China
email: fhanying@yahoo.com.cn
|
|---|
Return to the EJDE web page