Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 68, pp. 1-5.
Similarity solutions to evolution equations in one-dimensional interfaces
Mohammed Benlahsen, Ayman Eldoussouki, Mohammed Guedda, Mustapha Jazar
Abstract:
In this note, we study the evolution equation

which was introduced by Munoz-Garcia [9]
in the context of erosion by ion beam sputtering.
We obtain an analytic solution that has the similarity form,
which is used in obtaining the coarsening behavior.
This solution has amplitude and wavelength that increase
like
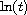 and
and
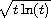 ,
respectively.
,
respectively.
Submitted April 15, 2011. Published May 20, 2011.
Math Subject Classifications: 70K42, 34A34, 35K55.
Key Words: Nonlinear dynamic; instability; similarity solution; coarsening.
Show me the PDF file (153 KB),
TEX file, and other files for this article.
 |
Mohammed Benlahsen
LPMC, Department of Physic, Université de Picardie Jules Verne
33, rue saint-Leu, Amiens, France
email: mohammed.benlahsen@u-picardie.fr
|
|---|
 |
Ayman Eldoussouki
LAMFA, CNRS UMR 6140, Department of Mathematics
Université de Picardie Jules Verne
33, rue saint-Leu, Amiens, France
email: ayman.eldoussouki@u-picardie.fr
|
|---|
 |
Mohammed Guedda
LAMFA, CNRS UMR 6140, Department of Mathematics
Université de Picardie Jules Verne
33, rue saint-Leu, Amiens, France
email: guedda@u-picardie.fr
|
|---|
 |
Mustapha Jazar
LaMA-Liban, Lebanese University
P.O. Box 37 Tripoli via Beirut, Lebanon
email: mjazar@laser-lb.org
|
|---|
Return to the EJDE web page

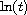 and
and
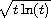 ,
respectively.
,
respectively.



