Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 51, pp. 1-19.
Second-order boundary estimates for solutions to singular
elliptic equations in borderline cases
Claudia Anedda, Giovanni Porru
Abstract:
Let
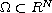 be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
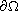 on the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the equation
on the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the equation
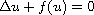 .
Under appropriate growth conditions on
.
Under appropriate growth conditions on
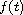 as t approaches zero,
we find asymptotic expansions up to the second order of the solution
in terms of the distance from x to the boundary
as t approaches zero,
we find asymptotic expansions up to the second order of the solution
in terms of the distance from x to the boundary
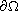 .
.
Submitted January 10, 2011. Published April 13, 2011.
Math Subject Classifications: 35B40, 35J67.
Key Words: Elliptic problems; singular equations;
second order boundary approximation.
Show me the PDF file (283 KB),
TEX file, and other files for this article.
 |
Claudia Anedda
Dipartimento di Matematica e Informatica
Universitá di Cagliari
Via Ospedale 72, 09124 Cagliari, Italy
email: canedda@unica.it
|
|---|
 |
Giovanni Porru
Dipartimento di Matematica e Informatica
Universitá di Cagliari
Via Ospedale 72, 09124 Cagliari, Italy
email: porru@unica.it
|
|---|
Return to the EJDE web page
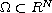 be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
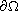 on the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the equation
on the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the equation
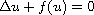 .
Under appropriate growth conditions on
.
Under appropriate growth conditions on
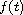 as t approaches zero,
we find asymptotic expansions up to the second order of the solution
in terms of the distance from x to the boundary
as t approaches zero,
we find asymptotic expansions up to the second order of the solution
in terms of the distance from x to the boundary
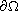 .
.

