Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 43, pp. 1-9.
Existence and multiplicity of solutions for divergence type
elliptic equations
Lin Zhao, Peihao Zhao, Xiaoxia Xie
Abstract:
We establish the existence and multiplicity of weak solutions
of a problem involving a uniformly convex elliptic operator
in divergence form.
We find one nontrivial solution by the mountain pass lemma,
when the nonlinearity has a
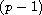 -superlinear
growth at infinity,
and two nontrivial solutions by minimization and mountain pass
when the nonlinear term has a
-superlinear
growth at infinity,
and two nontrivial solutions by minimization and mountain pass
when the nonlinear term has a
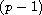 -sublinear
growth at infinity.
-sublinear
growth at infinity.
Submitted January 1, 2011. Published March 31, 2011.
Math Subject Classifications: 35A15, 35J20, 35J62.
Key Words: Nonlinear elliptic equations; uniformly convex;
mountain pass lemma; three critical points theorem.
Show me the PDF file (218 KB),
TEX file, and other files for this article.
 |
Lin Zhao
School of Mathematics and Statistics, Lanzhou University
Lanzhou, Gansu 730000, China
email: zhjz9332003@gmail.com
|
|---|
 |
Peihao Zhao
School of Mathematics and Statistics, Lanzhou University
Lanzhou, Gansu 730000, China
email: zhaoph@lzu.edu.cn
|
|---|
 |
Xiaoxia Xie
School of Mathematics and Statistics, Lanzhou University
Lanzhou, Gansu 730000, China
email: xiexx06@lzu.cn
|
|---|
Return to the EJDE web page
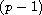 -superlinear
growth at infinity,
and two nontrivial solutions by minimization and mountain pass
when the nonlinear term has a
-superlinear
growth at infinity,
and two nontrivial solutions by minimization and mountain pass
when the nonlinear term has a
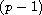 -sublinear
growth at infinity.
-sublinear
growth at infinity.


