Under the Keller-Osserman condition on
 ,
we show the existence
and nonexistence of entire solutions for the semilinear elliptic system
,
we show the existence
and nonexistence of entire solutions for the semilinear elliptic system
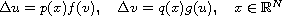 ,
where
,
where
 are continuous functions.
are continuous functions.
Zhijun Zhang, Yongxiu Shi, Yanxing Xue
Abstract:
Under the Keller-Osserman condition on
 ,
we show the existence
and nonexistence of entire solutions for the semilinear elliptic system
,
we show the existence
and nonexistence of entire solutions for the semilinear elliptic system
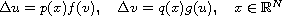 ,
where
,
where
 are continuous functions.
are continuous functions.
Submitted January 22, 2011. Published March 9, 2011.
Math Subject Classifications: 35J55, 35J60, 35J65.
Key Words: Semilinear elliptic systems; entire solutions; existence.
Show me the PDF file (223 KB), TEX file, and other files for this article.
 |
Zhijun Zhang School of Mathematics and Information Science Yantai University, Yantai, Shandong, 264005, China email: zhangzj@ytu.edu.cn |
|---|---|
 |
Yongxiu Shi School of Mathematics and Information Science Yantai University, Yantai, Shandong, 264005, China email: syxiu0926@126.com |
 |
Yanxing Xue School of Mathematics and Information Science Yantai University, Yantai, Shandong, 264005, China email: xiaoxue19870626@163.com |
Return to the EJDE web page