Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 161, pp. 1-21.
Regularity and symmetry of positive solutions to nonlinear
integral systems
Wanghe Yao, Xiaoli Chen, Jianfu Yang
Abstract:
In this article, we consider the regularity and symmetry of
positive solutions to the nonlinear integral system

for
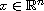 ,
where
,
where
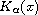 is the kernel of
the operator
is the kernel of
the operator
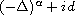 of order
of order
 ,
with
,
with
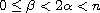 ,
,
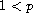 ,
,
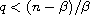 and
and
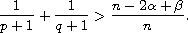
We show that positive solution pairs
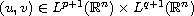 are locally Holder continuous in
are locally Holder continuous in
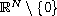 ,
radially symmetric about the origin, and strictly decreasing.
,
radially symmetric about the origin, and strictly decreasing.
Submitted July 9, 2011. Published December 7, 2011.
Math Subject Classifications: 35J25, 47G30, 35B45, 35J70.
Key Words: L-infinity bounds; Holder continuous;
radial symmetry; fractional Laplacian.
Show me the PDF file (328 KB),
TEX file, and other files for this article.
 |
Wanghe Yao
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: yaowanghe198610@sina.com
|
|---|
 |
Xiaoli Chen
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: littleli_chen@163.com
|
|---|
 |
Jianfu Yang
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
Return to the EJDE web page

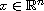 ,
where
,
where
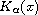 is the kernel of
the operator
is the kernel of
the operator
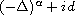 of order
of order
 ,
with
,
with
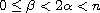 ,
,
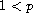 ,
,
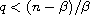 and
and
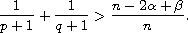
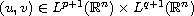 are locally Holder continuous in
are locally Holder continuous in
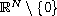 ,
radially symmetric about the origin, and strictly decreasing.
,
radially symmetric about the origin, and strictly decreasing.


