Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 147, pp. 1-5.
Krasnosel'skii fixed point theorem for dissipative operators
Tian Xiang
Abstract:
In this note, a sufficient condition guaranteing the existence of
fixed points in a nonempty, closed convex K for T+S is given,
where
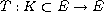 is dissipative and
is dissipative and
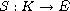 is condensing.
This may indicate a new direction of the Krasnoselskii type fixed
point theorem.
is condensing.
This may indicate a new direction of the Krasnoselskii type fixed
point theorem.
Submitted July 22, 2011. Published November 3, 2011.
Math Subject Classifications: 37C25, 47H09,47H10, 47H30.
Key Words: Dissipative operator; condensing operator; fixed point.
Show me the PDF file (166 KB),
TEX file, and other files for this article.
 |
Tian Xiang
Department of Mathematics,
Tulane University
New Orleans, LA 70118, USA
email: txiang@tulane.edu
|
|---|
Return to the EJDE web page
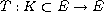 is dissipative and
is dissipative and
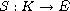 is condensing.
This may indicate a new direction of the Krasnoselskii type fixed
point theorem.
is condensing.
This may indicate a new direction of the Krasnoselskii type fixed
point theorem.
