Electron. J. Diff. Equ., Vol. 2011 (2011), No. 141, pp. 1-9.

Bifurcation from infinity and multiple solutions for first-order periodic boundary-value problems

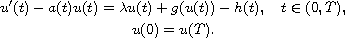
Zhenyan Wang, Chenghua Gao

Abstract:
In this article, we study the existence and multiplicity of solutions for the first-order periodic boundary-value problem
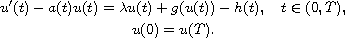
$$\displaylines{ u'(t)-a(t)u(t)=\lambda u(t)+g(u(t))-h(t), \quad t\in (0, T),\cr u(0)=u(T). }$$

Submitted September 6, 2011. Published October 28, 2011.
Math Subject Classifications: 34B18.
Key Words: First-order periodic problems; Landsman-Lazer type condition; Leray-Schauder degree; bifurcation; existence.

Show me the PDF file (217 KB), TEX file, and other files for this article.

Zhenyan Wang
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: wangzhenyan86714@163.com
Chenghua Gao
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: gaokuguo@163.com

Return to the EJDE web page