Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 14, pp. 1-14.
Positive solutions to generalized second-order three-point
integral boundary-value problems
Saowaluk Chasreechai, Jessada Tariboon
Abstract:
In this article, by using Krasnoselskii's fixed point theorem,
we obtain single and multiple positive solutions to the
nonlinear second-order three-point integral boundary value
problem
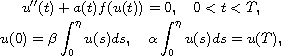
where
 ,
,
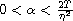 ,
,
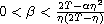 are given constants.
As an application, we give some examples that illustrate our results.
are given constants.
As an application, we give some examples that illustrate our results.
Submitted October 22, 2010. Published January 26, 2011.
Math Subject Classifications: 34B15, 34K10.
Key Words: Positive solution; three-point boundary value problem;
fixed point theorem; cone.
Show me the PDF file (245 KB),
TEX file, and other files for this article.
 |
Saowaluk Chasreechai
Department of Mathematics, Faculty of Applied Science
King Mongkut's University of Technology North Bangkok
Bangkok 10800, Thailand
email: slc@kmutnb.ac.th
|
|---|
 |
Jessada Tariboon
Department of Mathematics, Faculty of Applied Science
King Mongkut's University of Technology North Bangkok
Bangkok 10800, Thailand.
Centre of Excellence in Mathematics, CHE,
Sri Ayutthaya Road, Bangkok 10400, Thailand
email: jessadat@kmutnb.ac.th
|
|---|
Return to the EJDE web page
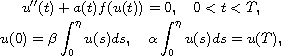
 ,
,
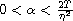 ,
,
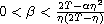 are given constants.
As an application, we give some examples that illustrate our results.
are given constants.
As an application, we give some examples that illustrate our results.

