A method is presented for proving the existence of solutions for boundary-value problems on the half line. The problems under study are nonlinear, nonautonomous systems of ODEs with the possibility of some prescribed value at
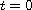 and with the condition that
solutions decay to zero as
and with the condition that
solutions decay to zero as
 grows large. The method relies
upon a topological degree for proper Fredholm maps.
Specific conditions are given to ensure that the boundary-value
problem corresponds to a functional equation that involves an
operator with the required smoothness, properness, and Fredholm
properties (including a calculable Fredholm index).
When the Fredholm index is zero and the solutions are bounded
a priori, then a solution exists. The method is applied
to obtain new existence results for systems of the form
grows large. The method relies
upon a topological degree for proper Fredholm maps.
Specific conditions are given to ensure that the boundary-value
problem corresponds to a functional equation that involves an
operator with the required smoothness, properness, and Fredholm
properties (including a calculable Fredholm index).
When the Fredholm index is zero and the solutions are bounded
a priori, then a solution exists. The method is applied
to obtain new existence results for systems of the form
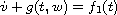 and
and
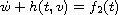 .
.
