We study the periodic boundary-value problem
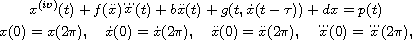
Under some resonant conditions on the asymptotic behaviour of the ratio
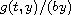 for
for
 .
Uniqueness of periodic
solutions is also examined.
.
Uniqueness of periodic
solutions is also examined.
Samuel A. Iyase
Abstract:
We study the periodic boundary-value problem
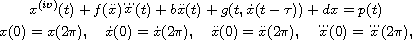
Under some resonant conditions on the asymptotic behaviour of the
ratio
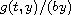 for
for
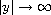 .
Uniqueness of periodic
solutions is also examined.
.
Uniqueness of periodic
solutions is also examined.
Submitted June 3, 2011. Published October 11, 2011.
Math Subject Classifications: 34B15.
Key Words: Periodic solution; uniqueness, uniqueness;
Carathoeodory conditions; fourth order ODE; delay
Show me the PDF file (189 KB), TEX file, and other files for this article.
 |
Samuel A. Iyase Department of Mathematics, Computer Science and Information Technology Igbinedion University, Okada, P.M.B. 0006 Benin City, Edo State, Nigeria email: driyase2011@yahoo.com, iyasesam@gmail.com |
|---|
Return to the EJDE web page