Electron. J. Diff. Equ., Vol. 2011 (2011), No. 128, pp. 1-7.

Periodic solutions for a second-order nonlinear neutral differential equation with variable delay

Abdelouaheb Ardjouni, Ahcene Djoudi

Abstract:
In this work, the hybrid fixed point theorem of Krasnoselskii is used to prove the existence of periodic solutions of the second-order nonlinear neutral differential equation
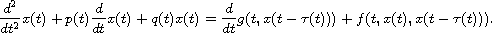
$$ \frac{d^2}{dt^2}x(t)+p(t)\frac{d}{dt}x(t)+q(t)x(t) =\frac{d}{dt}g(t,x(t-\tau(t)))+f(t,x(t),x(t-\tau(t))). $$
We transform the problem into an integral equation and uniqueness of the periodic solution, by means of the contraction mapping principle.

Submitted March 2, 2011. Published October 11, 2011.
Math Subject Classifications: 34K13, 34A34, 34K30, 34L30.
Key Words: Periodic solution; neutral differential equation; fixed point theorem.

Show me the PDF file (212 KB), TEX file, and other files for this article.

Abdelouaheb Ardjouni
Department of Mathematics, Faculty of Sciences
University of Annaba, P.O. Box 12 Annaba, Algeria
email: abd_ardjouni@yahoo.fr
  Ahcene Djoudi
Department of Mathematics, Faculty of Sciences
University of Annaba, P.O. Box 12 Annaba, Algeria
email: adjoudi@yahoo.com

Return to the EJDE web page