Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 127, pp. 1-14.
Decay rates of magnetoelastic waves in an unbounded conductive medium
Ruy Coimbra Charao, Jauber Cavalcante Oliveira,
Gustavo Perla Menzala
Abstract:
We study the uniform decay of the total energy of solutions
for a system in magnetoelasticity with localized damping near
infinity in an exterior 3-D domain. Using appropriate multipliers
and recent work by Charao and Ikekata [3], we conclude that
the energy decays at the same rate as
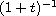 when
when
 .
.
Submitted September 23, 2011. Published October 11, 2011.
Math Subject Classifications: 35B40, 35Q60, 36Q99.
Key Words: Magnetoelastic waves; exterior domain; localized damping;
energy decay.
Show me the PDF file (272 KB),
TEX file, and other files for this article.
 |
Ruy Coimbra Charão
Department of Mathematics
Federal University of Santa Catarina
CEP 88040-900, Florianópolis, SC, Brazil
email: ruycharao@gmail.com
|
|---|
 |
Jáuber Cavalcante Oliveira
Department of Mathematics
Federal University of Santa Catarina
CEP 88040-900, Florianópolis, SC, Brazil
email: jauber@mtm.ufsc.br
|
|---|
 |
Gustavo Perla Menzala
Department of Mathematics
Federal University of Santa Catarina
CEP 88040-900, Florianópolis, SC, Brazil
email: perla@lncc.br
|
|---|
Return to the EJDE web page
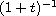 when
when
 .
.


