Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 125, pp. 1-14.
Kwong-Wong-type integral equation on time scales
Baoguo Jia
Abstract:
Consider the second-order nonlinear dynamic equation
![$$
[r(t)x^\Delta(\rho(t))]^\Delta+p(t)f(x(t))=0,
$$](gifs/aa.gif)
where
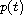 is the backward jump operator.
We obtain a Kwong-Wong-type integral equation, that is:
If
is the backward jump operator.
We obtain a Kwong-Wong-type integral equation, that is:
If
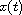 is a nonoscillatory solution of the above equation on
is a nonoscillatory solution of the above equation on
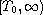 ,
then the integral equation
,
then the integral equation
![$$
\frac{r^\sigma(t)x^\Delta(t)}{f(x^\sigma(t))}
=P^\sigma(t)+\int^\infty_{\sigma(t)}\frac{r^\sigma(s)
[\int^1_0f'(x_h(s))dh][x^\Delta(s)]^2}{f(x(s))
f(x^\sigma(s))}\Delta s
$$](gifs/ae.gif)
is satisfied for
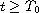 ,
where
,
where
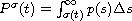 ,
and
,
and
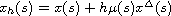 .
As an application, we show that the superlinear dynamic equation
.
As an application, we show that the superlinear dynamic equation
![$$
[r(t)x^{\Delta}(\rho(t))]^\Delta+p(t)f(x(t))=0,
$$](gifs/ai.gif)
is oscillatory, under certain conditions.
Submitted July 21, 2011. Published September 29, 2011.
Math Subject Classifications: 34K11, 39A10, 39A99.
Key Words: Nonlinear dynamic equation; integral equation;
nonoscillatory solution.
Show me the PDF file (263 KB),
TEX file, and other files for this article.
 |
Baoguo Jia
School of Mathematics and Computer Science
Zhongshan University,
Guangzhou, 510275, China
email: mcsjbg@mail.sysu.edu.cn
|
|---|
Return to the EJDE web page
![$$
[r(t)x^\Delta(\rho(t))]^\Delta+p(t)f(x(t))=0,
$$](gifs/aa.gif)
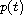 is the backward jump operator.
We obtain a Kwong-Wong-type integral equation, that is:
If
is the backward jump operator.
We obtain a Kwong-Wong-type integral equation, that is:
If
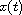 is a nonoscillatory solution of the above equation on
is a nonoscillatory solution of the above equation on
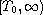 ,
then the integral equation
,
then the integral equation
![$$
\frac{r^\sigma(t)x^\Delta(t)}{f(x^\sigma(t))}
=P^\sigma(t)+\int^\infty_{\sigma(t)}\frac{r^\sigma(s)
[\int^1_0f'(x_h(s))dh][x^\Delta(s)]^2}{f(x(s))
f(x^\sigma(s))}\Delta s
$$](gifs/ae.gif)
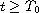 ,
where
,
where
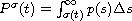 ,
and
,
and
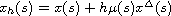 .
As an application, we show that the superlinear dynamic equation
.
As an application, we show that the superlinear dynamic equation
![$$
[r(t)x^{\Delta}(\rho(t))]^\Delta+p(t)f(x(t))=0,
$$](gifs/ai.gif)
