Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 121, pp. 1-16.
Computation of rational solutions for a
first-order nonlinear differential equation
Djilali Behloul, Sui Sun Cheng
Abstract:
In this article, we study differential equations of
the form
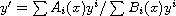 which
can be elliptic, hyperbolic, parabolic, Riccati, or quasi-linear.
We show how rational solutions can be computed in a systematic manner.
Such results are most likely to find applications in the theory of
limit cycles as indicated by Gine et al [4].
which
can be elliptic, hyperbolic, parabolic, Riccati, or quasi-linear.
We show how rational solutions can be computed in a systematic manner.
Such results are most likely to find applications in the theory of
limit cycles as indicated by Gine et al [4].
Submitted August 23, 2011. Published September 19, 2011.
Math Subject Classifications: 34A05.
Key Words: Polynomial solution; rational solution; nonlinear differential
equation.
Show me the PDF file (261 KB),
TEX file, and other files for this article.
 |
Djilali Behloul
Faculté Génie Electrique
Département informatique, USTHB, BP32
El Alia, Bab Ezzouar, 16111, Algiers, Algeria
email: dbehloul@yahoo.fr
|
|---|
 |
Sui Sun Cheng
Department of Mathematics, Hua University
Hsinchu 30043, Taiwan
email: sscheng@math.nthu.edu.tw
|
|---|
Return to the EJDE web page
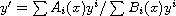 which
can be elliptic, hyperbolic, parabolic, Riccati, or quasi-linear.
We show how rational solutions can be computed in a systematic manner.
Such results are most likely to find applications in the theory of
limit cycles as indicated by Gine et al [4].
which
can be elliptic, hyperbolic, parabolic, Riccati, or quasi-linear.
We show how rational solutions can be computed in a systematic manner.
Such results are most likely to find applications in the theory of
limit cycles as indicated by Gine et al [4].

