Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 115, pp. 1-11.
Compactness result for periodic structures and its application
to the homogenization of a diffusion-convection equation
Anvarbek Meirmanov, Reshat Zimin
Abstract:
We prove the strong compactness of the sequence
 in
in
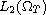 ,
,
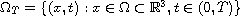 ,
bounded in
,
bounded in
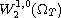 with the sequence of time derivative
with the sequence of time derivative
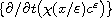 bounded in the space
bounded in the space
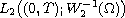 .
As an application we consider the homogenization of a
diffusion-convection equation with a
sequence of divergence-free velocities
.
As an application we consider the homogenization of a
diffusion-convection equation with a
sequence of divergence-free velocities
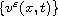 weakly convergent in
weakly convergent in
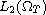 .
.
Submitted April 10, 2011. Published September 6, 2011.
Math Subject Classifications: 35B27, 46E35, 76R99.
Key Words: Weak, strong and two-scale convergence; homogenization;
diffusion-convection.
Show me the PDF file (251 KB),
TEX file, and other files for this article.
 |
Anvarbek M. Meirmanov
Department of mahtematics,
Belgorod State University
ul.Pobedi 85, 308015 Belgorod, Russia
email: meirmanov@bsu.edu.ru
|
|---|
 |
Reshat Zimin
Department of mahtematics,
Belgorod State University
ul.Pobedi 85, 308015 Belgorod, Russia
email: reshat85@mail.ru
|
|---|
Return to the EJDE web page
 in
in
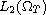 ,
,
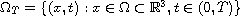 ,
bounded in
,
bounded in
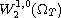 with the sequence of time derivative
with the sequence of time derivative
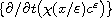 bounded in the space
bounded in the space
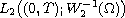 .
As an application we consider the homogenization of a
diffusion-convection equation with a
sequence of divergence-free velocities
.
As an application we consider the homogenization of a
diffusion-convection equation with a
sequence of divergence-free velocities
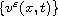 weakly convergent in
weakly convergent in
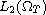 .
.

