Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 112, pp. 1-34.
Periodic boundary-value problems and the Dancer-Fucik
spectrum under conditions of resonance
David A. Bliss, James Buerger, Adolfo J. Rumbos
Abstract:
We prove the existence of solutions to the nonlinear
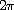 -periodic
problem
-periodic
problem
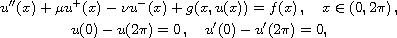
where the point
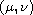 lies in the Dancer-Fucik spectrum, with
lies in the Dancer-Fucik spectrum, with
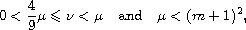
for some natural number m, and the nonlinearity
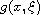 is bounded
with primitive,
is bounded
with primitive,
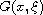 ,
satisfying a
Landesman-Lazer type condition introduced by Tomiczek in 2005.
We use variational methods based on the generalization of the
Saddle Point Theorem of Rabinowitz.
,
satisfying a
Landesman-Lazer type condition introduced by Tomiczek in 2005.
We use variational methods based on the generalization of the
Saddle Point Theorem of Rabinowitz.
Submitted November 10, 2010. Published August 29, 2011.
Math Subject Classifications: 34B15, 34K13, 35A15.
Key Words: Resonance; jumping nonlinearities; Dancer-Fucik spectrum;
saddle point theorem.
Show me the PDF file (483 KB),
TEX file, and other files for this article.
 |
David A. Bliss
School of Mathematical Sciences, Claremont Graduate University
Claremont, CA 91711, USA
david.a.bliss@jpl.nasa.gov
|
|---|
| |
James Buerger
Department of Mathematics, Pomona College
Claremont, CA 91711, USA
email: jbuerg127@gmail.com
|
|---|
 |
Adolfo J. Rumbos
Department of Mathematics, Pomona College
Claremont, CA 91711, USA
email: arumbos@pomona.edu
|
|---|
Return to the EJDE web page
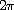 -periodic
problem
-periodic
problem
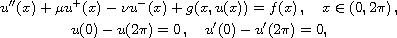
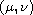 lies in the Dancer-Fucik spectrum, with
lies in the Dancer-Fucik spectrum, with
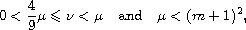
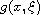 is bounded
with primitive,
is bounded
with primitive,
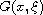 ,
satisfying a
Landesman-Lazer type condition introduced by Tomiczek in 2005.
We use variational methods based on the generalization of the
Saddle Point Theorem of Rabinowitz.
,
satisfying a
Landesman-Lazer type condition introduced by Tomiczek in 2005.
We use variational methods based on the generalization of the
Saddle Point Theorem of Rabinowitz.

