Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 109, pp. 1-12.
Resolvent estimates for elliptic systems in
function spaces of higher regularity
Robert Denk, Michael Dreher
Abstract:
We consider parameter-elliptic boundary value problems and
uniform a priori estimates in
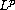 -Sobolev
spaces of
Bessel potential and Besov type. The problems considered are
systems of uniform order and mixed-order systems
(Douglis-Nirenberg systems). It is shown that compatibility
conditions on the data are necessary for such estimates to hold.
In particular, we consider the realization of the boundary value
problem as an unbounded operator with the ground space being a
closed subspace of a Sobolev space and give necessary and sufficient
conditions for the realization to generate an analytic semigroup.
-Sobolev
spaces of
Bessel potential and Besov type. The problems considered are
systems of uniform order and mixed-order systems
(Douglis-Nirenberg systems). It is shown that compatibility
conditions on the data are necessary for such estimates to hold.
In particular, we consider the realization of the boundary value
problem as an unbounded operator with the ground space being a
closed subspace of a Sobolev space and give necessary and sufficient
conditions for the realization to generate an analytic semigroup.
Submitted January 11, 2011. Published August 25, 2011.
Math Subject Classifications: 35G45, 47D06.
Key Words: Parameter-ellipticity; Douglis-Nirenberg systems;
analytic semigroups.
Show me the PDF file (261 KB),
TEX file, and other files for this article.
 |
Robert Denk
Department of Mathematics and Statistics
University of Konstanz
78457 Konstanz, Germany
email: robert.denk@uni-konstanz.de
|
|---|
 |
Michael Dreher
Department of Mathematics and Statistics
University of Konstanz
78457 Konstanz, Germany
email: michael.dreher@uni-konstanz.de
|
|---|
Return to the EJDE web page
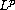 -Sobolev
spaces of
Bessel potential and Besov type. The problems considered are
systems of uniform order and mixed-order systems
(Douglis-Nirenberg systems). It is shown that compatibility
conditions on the data are necessary for such estimates to hold.
In particular, we consider the realization of the boundary value
problem as an unbounded operator with the ground space being a
closed subspace of a Sobolev space and give necessary and sufficient
conditions for the realization to generate an analytic semigroup.
-Sobolev
spaces of
Bessel potential and Besov type. The problems considered are
systems of uniform order and mixed-order systems
(Douglis-Nirenberg systems). It is shown that compatibility
conditions on the data are necessary for such estimates to hold.
In particular, we consider the realization of the boundary value
problem as an unbounded operator with the ground space being a
closed subspace of a Sobolev space and give necessary and sufficient
conditions for the realization to generate an analytic semigroup.

