Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 104, pp. 1-19.
Existence of solutions of systems of Volterra integral equations
via Brezis-Browder arguments
Ravi P. Agarwal, Donal O'Regan, Patricia J. Y. Wong
Abstract:
We consider two systems of Volterra integral equations

where t is in the closed interval
![$[0,T]$](gifs/ab.gif) ,
or in
the half-open interval
,
or in
the half-open interval
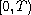 .
By an argument originated from
Brezis and Browder [8], criteria are offered for the existence
of solutions of the systems of Volterra integral equations. We
further establish the existence of constant-sign solutions,
which include positive solutions (the usual consideration) as
a special case. Some examples are also presented to illustrate
the results obtained.
.
By an argument originated from
Brezis and Browder [8], criteria are offered for the existence
of solutions of the systems of Volterra integral equations. We
further establish the existence of constant-sign solutions,
which include positive solutions (the usual consideration) as
a special case. Some examples are also presented to illustrate
the results obtained.
Submitted April 26, 2011. Published August 16, 2011.
Math Subject Classifications: 45B05, 45G15, 45M20.
Key Words: System of Volterra integral equations; Brezis-Browder argument.
Show me the PDF file (349 KB),
TEX file, and other files for this article.
 |
Ravi P. Agarwal
Department of Mathematics, Texas A&M University - Kingsville
Kingsville, Texas 78363-8202, USA
email: agarwal@tamuk.edu
|
|---|
 |
Donal O'Regan
Department of Mathematics, National University of Ireland
Galway, Ireland
email: donal.oregan@nuigalway.ie
|
|---|
 |
Patricia J. Y. Wong
School of Electrical and Electronic Engineering
Nanyang Technological University
50 Nanyang Avenue, Singapore 639798, Singapore
email: ejywong@ntu.edu.sg
|
|---|
Return to the EJDE web page

![$[0,T]$](gifs/ab.gif) ,
or in
the half-open interval
,
or in
the half-open interval
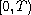 .
By an argument originated from
Brezis and Browder [8], criteria are offered for the existence
of solutions of the systems of Volterra integral equations. We
further establish the existence of constant-sign solutions,
which include positive solutions (the usual consideration) as
a special case. Some examples are also presented to illustrate
the results obtained.
.
By an argument originated from
Brezis and Browder [8], criteria are offered for the existence
of solutions of the systems of Volterra integral equations. We
further establish the existence of constant-sign solutions,
which include positive solutions (the usual consideration) as
a special case. Some examples are also presented to illustrate
the results obtained.


