Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 101, pp. 1-9.
Oscillation theorems for second-order neutral functional dynamic
equations on time scales
Cunchen Gao, Tongxing Li, Shuhong Tang, Ethiraju Thandapani
Abstract:
In this article, we obtain several comparison theorems for the
second-order neutral dynamic equation
![$$
\Big(r(t)\big([x(t)+p(t)x(\tau(t))]^\Delta\big)^\gamma\Big)^\Delta
+q_1(t)x^\lambda(\delta(t))+q_2(t)x^\beta(\eta(t))=0,
$$](gifs/aa.gif)
where
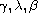 are ratios of positive
odd integers. We compare such equation with the first-order
dynamic inequalities in the sense that the absence of the
eventually positive solutions of these first-order inequalities
implies the oscillation of the studied equation.
are ratios of positive
odd integers. We compare such equation with the first-order
dynamic inequalities in the sense that the absence of the
eventually positive solutions of these first-order inequalities
implies the oscillation of the studied equation.
Submitted March 21, 2011. Published August 10, 2011.
Math Subject Classifications: 34K11, 39A21, 34N05.
Key Words: Oscillation; neutral functional dynamic equation;
comparison theorem; time scales.
Show me the PDF file (222 KB),
TEX file, and other files for this article.
 |
Cunchen Gao
College of Information Science and Engineering
Ocean University of China, Qingdao, Shandong 266100, China
email: ccgao@ouc.edu.cn
|
|---|
 |
Tongxing Li
School of Control Science and Engineering
Shandong University, Jinan, Shandong 250061, China
email: litongx2007@hotmail.com
|
|---|
 |
Shuhong Tang
School of Information and Control Engineering
Weifang University, Weifang, Shandong 261061, China
email: wfxytang@163.com
|
|---|
 |
Ethiraju Thandapani
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai, India
email: ethandapani@yahoo.co.in
|
|---|
Return to the EJDE web page
![$$
\Big(r(t)\big([x(t)+p(t)x(\tau(t))]^\Delta\big)^\gamma\Big)^\Delta
+q_1(t)x^\lambda(\delta(t))+q_2(t)x^\beta(\eta(t))=0,
$$](gifs/aa.gif)
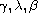 are ratios of positive
odd integers. We compare such equation with the first-order
dynamic inequalities in the sense that the absence of the
eventually positive solutions of these first-order inequalities
implies the oscillation of the studied equation.
are ratios of positive
odd integers. We compare such equation with the first-order
dynamic inequalities in the sense that the absence of the
eventually positive solutions of these first-order inequalities
implies the oscillation of the studied equation.



