Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 84, pp. 1-6.
Uniqueness and parameter dependence of solutions
of fourth-order four-point nonhomogeneous BVPs
Jian-Ping Sun, Xiao-Yun Wang
Abstract:
In this article, we investigate the fourth-order
four-point nonhomogeneous Sturm-Liouville boundary-value
problem
![$$\displaylines{
u^{(4)}(t)=f(t,u(t)),\quad t\in [0,1], \cr
\alpha u(0)-\beta u'(0)=\gamma u(1)+\delta u'(1)=0, \cr
au''(\xi _1)-bu'''(\xi _1)=-\lambda ,\quad
cu''(\xi _2)+du'''(\xi _2)=-\mu ,
}$$](gifs/aa.gif)
where
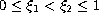 and
and
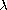 and
and
 are
nonnegative parameters. We obtain sufficient conditions for
the existence and uniqueness of positive solutions.
The dependence of the solution on the parameters
are
nonnegative parameters. We obtain sufficient conditions for
the existence and uniqueness of positive solutions.
The dependence of the solution on the parameters
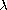 and
and
 is also studied.
is also studied.
Submitted September 21, 2009. Published June 18, 2010.
Math Subject Classifications: 34B08, 34B10.
Key Words: Nonhomogeneous; fourth-order; four-point; Sturm-Liouville;
boundary-value problem; positive solution;
uniqueness; dependence on parameter
Show me the PDF file (183 KB),
TEX file, and other files for this article.
 |
Jian-Ping Sun
Department of Applied Mathematics,
Lanzhou University of Technology
Lanzhou, Gansu 730050, China
email: jpsun@lut.cn
|
|---|
 |
Xiao-Yun Wang
Department of Applied Mathematics,
Lanzhou University of Technology
Lanzhou, Gansu 730050, China
email: catherine699@163.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
u^{(4)}(t)=f(t,u(t)),\quad t\in [0,1], \cr
\alpha u(0)-\beta u'(0)=\gamma u(1)+\delta u'(1)=0, \cr
au''(\xi _1)-bu'''(\xi _1)=-\lambda ,\quad
cu''(\xi _2)+du'''(\xi _2)=-\mu ,
}$$](gifs/aa.gif)
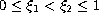 and
and
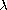 and
and
 are
nonnegative parameters. We obtain sufficient conditions for
the existence and uniqueness of positive solutions.
The dependence of the solution on the parameters
are
nonnegative parameters. We obtain sufficient conditions for
the existence and uniqueness of positive solutions.
The dependence of the solution on the parameters
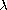 and
and
 is also studied.
is also studied.

