Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 77, pp. 1-12.
Infinity Laplace equation with non-trivial right-hand side
Guozhen Lu, Peiyong Wang
Abstract:
We analyze the set of continuous viscosity solutions of
the infinity Laplace equation
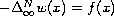 ,
with generally sign-changing right-hand side in a bounded domain.
The existence of a least and a greatest continuous viscosity
solutions, up to the boundary, is proved through a Perron's
construction by means of a strict comparison principle. These
extremal solutions are proved to be absolutely extremal solutions.
,
with generally sign-changing right-hand side in a bounded domain.
The existence of a least and a greatest continuous viscosity
solutions, up to the boundary, is proved through a Perron's
construction by means of a strict comparison principle. These
extremal solutions are proved to be absolutely extremal solutions.
Submitted July 2, 2009. Published June 8, 2010.
Math Subject Classifications: 35J70, 35B35.
Key Words: Infinity Laplace equation; inhomogeneous equation;
viscosity solutions; least solution; greatest solution;
strict comparison principle; existence; uniqueness;
local Lipschitz continuity.
Show me the PDF file (246 KB),
TEX file, and other files for this article.
 |
Guozhen Lu
Department of Mathematics,
Wayne State University
656 W. Kirby, 1150 FAB
Detroit, MI 48202, USA
email: gzlu@math.wayne.edu
|
|---|
 |
Peiyong Wang
Department of Mathematics,
Wayne State University
656 W. Kirby, 1150 FAB
Detroit, MI 48202, USA
email: pywang@math.wayne.edu
|
|---|
Return to the EJDE web page
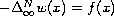 ,
with generally sign-changing right-hand side in a bounded domain.
The existence of a least and a greatest continuous viscosity
solutions, up to the boundary, is proved through a Perron's
construction by means of a strict comparison principle. These
extremal solutions are proved to be absolutely extremal solutions.
,
with generally sign-changing right-hand side in a bounded domain.
The existence of a least and a greatest continuous viscosity
solutions, up to the boundary, is proved through a Perron's
construction by means of a strict comparison principle. These
extremal solutions are proved to be absolutely extremal solutions.

