Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 73, pp. 1-9.
Oscillation criteria for forced second-order mixed
type quasilinear delay differential equations
Sowdaiyan Murugadass, Ethiraju Thandapani, Sandra Pinelas
Abstract:
This article presents new oscillation criteria
for the second-order delay differential equation

where
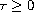 ,
,
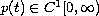 ,
,
 ,
,
 ,
,
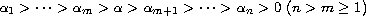 ,
,
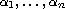 and
and
 are ratio of odd positive integers. Without assuming that
are ratio of odd positive integers. Without assuming that
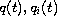 and
and
 are nonnegative, the results in [6,8]
have been extended and a mistake in the proof of the
results in [3] is corrected.
are nonnegative, the results in [6,8]
have been extended and a mistake in the proof of the
results in [3] is corrected.
Submitted January 10, 2010. Published May 19, 2010.
Math Subject Classifications: 34K11, 34C55.
Key Words: Interval oscillation; quasilinear delay differential equation;
second order.
Show me the PDF file (233 KB),
TEX file, and other files for this article.
 |
Sowdaiyan Murugadass
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai - 600005, India
email: murugadasssm@gmail.com
|
|---|
 |
Ethiraju Thandapani
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai - 600005, India
email: ethandapani@yahoo.co.in
|
|---|
 |
Sandra Pinelas
Departamento de Matemática
Universidade dos Açores, Portugal
email: sandra.pinelas@clix.pt
|
|---|
Return to the EJDE web page

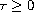 ,
,
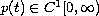 ,
,
 ,
,
 ,
,
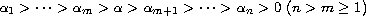 ,
,
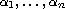 and
and
 are ratio of odd positive integers. Without assuming that
are ratio of odd positive integers. Without assuming that
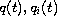 and
and
 are nonnegative, the results in [6,8]
have been extended and a mistake in the proof of the
results in [3] is corrected.
are nonnegative, the results in [6,8]
have been extended and a mistake in the proof of the
results in [3] is corrected.


