Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 69, pp. 1-8.
Almost automorphic solutions of neutral functional
differential equations
Gisele Massengo Mophou, Gaston M. N'Guerekata
Abstract:
In this article, we prove the existence and uniqueness of
almost automorphic solutions to the non-autonomous evolution
equation
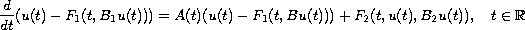
where
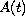 generates a hyperbolic evolution family
generates a hyperbolic evolution family
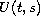 (not necessarily periodic) in a Banach space, and
(not necessarily periodic) in a Banach space, and
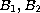 are bounded linear operators. The results are obtained by means
of fixed point methods.
are bounded linear operators. The results are obtained by means
of fixed point methods.
Submitted May 25, 2009. Published May 17, 2010.
Math Subject Classifications: 34K05, 34A12, 34A40.
Key Words: Neutral differential equation; almost automorphic functions;
almost periodic functions; exponentially stable semigroup;
semigroup of linear operators.
Show me the PDF file (210 KB),
TEX file, and other files for this article.
 |
Gisèle M. Mophou
Département de Mathématiques et Informatique
Université des Antilles et de La Guyane, Campus Fouillole 97159
Pointe-à-Pitre Guadeloupe (FWI)
email: gmophou@univ-ag.fr
|
|---|
 |
Gaston M. N'Guérékata
Department of Mathematics
Morgan State University
1700 E. Cold Spring Lane,
Baltimore, MD 21251, USA
email: Gaston.N'Guerekata@morgan.edu, nguerekata@aol.com |
|---|
Return to the EJDE web page
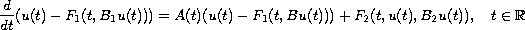
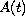 generates a hyperbolic evolution family
generates a hyperbolic evolution family
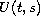 (not necessarily periodic) in a Banach space, and
(not necessarily periodic) in a Banach space, and
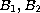 are bounded linear operators. The results are obtained by means
of fixed point methods.
are bounded linear operators. The results are obtained by means
of fixed point methods.

