Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 65, pp. 1-12.
Growth of solutions of higher-order linear
differential equations
Karima Hamani
Abstract:
In this article, we study the growth of
solutions of the linear differential equation
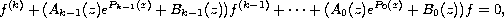
where
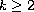 is an integer,
is an integer,
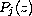 are nonconstant
polynomials and
are nonconstant
polynomials and
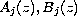 are entire functions,
not identically zero. We determine the hyper-order of these
solutions, under certain conditions.
are entire functions,
not identically zero. We determine the hyper-order of these
solutions, under certain conditions.
Submitted February 3, 2010. Published May 8, 2010.
Math Subject Classifications: 34A20, 30D35.
Key Words: Linear differential equation; entire function;
hyper-order.
Show me the PDF file (256 KB),
TEX file, and other files for this article.
 |
Karima Hamani
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem, B. P. 227 Mostaganem, Algeria
email: hamanikarima@yahoo.fr
|
|---|
Return to the EJDE web page
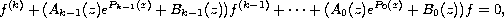
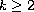 is an integer,
is an integer,
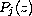 are nonconstant
polynomials and
are nonconstant
polynomials and
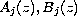 are entire functions,
not identically zero. We determine the hyper-order of these
solutions, under certain conditions.
are entire functions,
not identically zero. We determine the hyper-order of these
solutions, under certain conditions.
