Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 61, pp. 1-23.
Existence and concentration of positive solutions for a
quasilinear elliptic equation in R
Elisandra Gloss
Abstract:
We study the existence and concentration of positive
solutions for the quasilinear elliptic equation
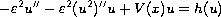
in
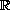 as
as
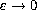 ,
where the potential
,
where the potential
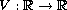 has a positive infimum and
has a positive infimum and
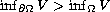 for some bounded domain
for some bounded domain
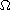 in
in
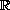 , and
, and
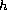 is a nonlinearity
without having growth conditions such as Ambrosetti-Rabinowitz.
is a nonlinearity
without having growth conditions such as Ambrosetti-Rabinowitz.
Submitted January 16, 2010. Published May 5, 2010.
Math Subject Classifications: 35J20, 35J62.
Key Words: Schrodinger equation; quasilinear equation;
concentration; variational methods.
Show me the PDF file (342 KB),
TEX file, and other files for this article.
 |
Elisandra Gloss
Departamento de Matemática
Universidade Federal da Paraíba
58000-000, João Pessoa - PB, Brazil
email: elisandra@mat.ufpb.br
|
|---|
Return to the EJDE web page
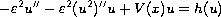
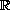 as
as
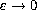 ,
where the potential
,
where the potential
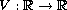 has a positive infimum and
has a positive infimum and
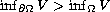 for some bounded domain
for some bounded domain
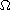 in
in
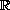 , and
, and
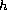 is a nonlinearity
without having growth conditions such as Ambrosetti-Rabinowitz.
is a nonlinearity
without having growth conditions such as Ambrosetti-Rabinowitz.
