Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 56, pp. 1-16.
Existence and multiplicity of solutions to elliptic problems
with discontinuities and free boundary conditions
Sabri Bensid, Sidi Mohammed Bouguima
Abstract:
We study the nonlinear elliptic problem with discontinuous nonlinearity
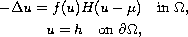
where
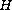 is the Heaviside unit function,
is the Heaviside unit function,
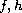 are given functions and
are given functions and
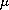 is a positive real parameter. The domain
is a positive real parameter. The domain
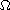 is the unit ball in
is the unit ball in
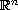 with
with
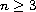 .
We show the existence of a positive
solution
.
We show the existence of a positive
solution
 and a hypersurface separating the region where
and a hypersurface separating the region where
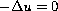 from the region where
from the region where
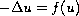 .
Our method relies
on the implicit function theorem and bifurcation analysis.
.
Our method relies
on the implicit function theorem and bifurcation analysis.
Submitted February 22, 2010. Published April 19, 2010.
Math Subject Classifications: 34R35, 35J25.
Key Words: Green function; maximum principle; bifurcation;
free boundary problem.
Show me the PDF file (273 KB),
TEX file, and other files for this article.
 |
Sabri Bensid
Department of Mathematics, Faculty of Sciences
University of Tlemcen,
B.P. 119, Tlemcen 13000, Algeria
email: edp_sabri@yahoo.fr
|
|---|
 |
Sidi Mohammed Bouguima
Department of Mathematics, Faculty of Sciences
University of Tlemcen,
B.P. 119, Tlemcen 13000, Algeria
email: bouguima@yahoo.fr
|
|---|
Return to the EJDE web page
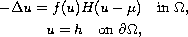
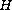 is the Heaviside unit function,
is the Heaviside unit function,
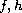 are given functions and
are given functions and
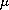 is a positive real parameter. The domain
is a positive real parameter. The domain
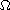 is the unit ball in
is the unit ball in
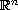 with
with
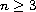 .
We show the existence of a positive
solution
.
We show the existence of a positive
solution
 and a hypersurface separating the region where
and a hypersurface separating the region where
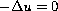 from the region where
from the region where
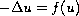 .
Our method relies
on the implicit function theorem and bifurcation analysis.
.
Our method relies
on the implicit function theorem and bifurcation analysis.

