Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 48, pp. 1-14.
Green function and Fourier transform for o-plus operators
Wanchak Satsanit
Abstract:
In this article, we study the o-plus operator defined by
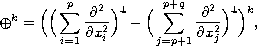
where
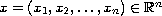 ,
,
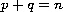 ,
and
,
and
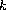 is a nonnegative integer. Firstly, we studied the
elementary solution for the
is a nonnegative integer. Firstly, we studied the
elementary solution for the
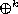 operator
and then this solution is related to the solution of the wave
and the Laplacian equations. Finally, we studied the Fourier
transform of the elementary solution and also the Fourier transform
of its convolution.
operator
and then this solution is related to the solution of the wave
and the Laplacian equations. Finally, we studied the Fourier
transform of the elementary solution and also the Fourier transform
of its convolution.
Submitted January 8, 2010. Published April 6, 2010.
Math Subject Classifications: 46F10, 46F12.
Key Words: Fourier transform; diamond operator; tempered distribution.
Show me the PDF file (256 KB),
TEX file, and other files for this article.
 |
Wanchak Satsanit
Faculty of Science, Department of Mathematics
Maejo University
Nong Han, San Sai,
Chiang Mai, 50290 Thailand
email: aunphue@live.com
|
|---|
Return to the EJDE web page
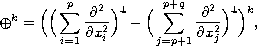
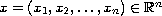 ,
,
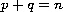 ,
and
,
and
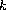 is a nonnegative integer. Firstly, we studied the
elementary solution for the
is a nonnegative integer. Firstly, we studied the
elementary solution for the
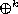 operator
and then this solution is related to the solution of the wave
and the Laplacian equations. Finally, we studied the Fourier
transform of the elementary solution and also the Fourier transform
of its convolution.
operator
and then this solution is related to the solution of the wave
and the Laplacian equations. Finally, we studied the Fourier
transform of the elementary solution and also the Fourier transform
of its convolution.
