Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 44, pp. 1-9.
Existence and multiplicity of solutions for a differential
inclusion problem involving the p(x)-Laplacian
Guowei Dai
Abstract:
In this article we consider the differential inclusion
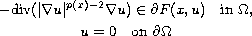
which involves the
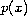 -Laplacian.
By applying the nonsmooth Mountain Pass Theorem, we obtain at
least one nontrivial solution; and by applying the
symmetric Mountain Pass Theorem, we obtain k-pairs of
nontrivial solutions in
-Laplacian.
By applying the nonsmooth Mountain Pass Theorem, we obtain at
least one nontrivial solution; and by applying the
symmetric Mountain Pass Theorem, we obtain k-pairs of
nontrivial solutions in
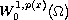 .
.
Submitted December 31, 2009. Published March 26, 2010.
Math Subject Classifications: 35J20, 35J70, 35R70.
Key Words: p(x)-Laplacian; nonsmooth mountain pass theorem;
differential inclusion.
Show me the PDF file (240 KB),
TEX file, and other files for this article.
 |
Guowei Dai
Department of Mathematics, Northwest Normal University
Lanzhou, 730070, China
email: daigw06@lzu.cn
|
|---|
Return to the EJDE web page
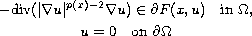
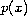 -Laplacian.
By applying the nonsmooth Mountain Pass Theorem, we obtain at
least one nontrivial solution; and by applying the
symmetric Mountain Pass Theorem, we obtain k-pairs of
nontrivial solutions in
-Laplacian.
By applying the nonsmooth Mountain Pass Theorem, we obtain at
least one nontrivial solution; and by applying the
symmetric Mountain Pass Theorem, we obtain k-pairs of
nontrivial solutions in
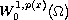 .
.
