Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 28, pp. 1-9.
Compactness results for Ginzburg-Landau type functionals with
general potentials
Matthias Kurzke
Abstract:
We study compactness and
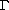 -convergence for Ginzburg-Landau
type functionals. We only assume that the
potential is continuous and positive definite close to one
circular well, but allow large zero sets inside the well.
We show that the relaxation of the assumptions does not change
the results to leading order unless the energy is very large.
-convergence for Ginzburg-Landau
type functionals. We only assume that the
potential is continuous and positive definite close to one
circular well, but allow large zero sets inside the well.
We show that the relaxation of the assumptions does not change
the results to leading order unless the energy is very large.
Submitted September 22, 2009. Published February 18, 2010.
Math Subject Classifications: 35J50, 35B25.
Key Words: Gamma-convergence; compactness for Jacobians;
Ginzburg-Landau functional.
Show me the PDF file (233 KB),
TEX file, and other files for this article.
 |
Matthias Kurzke
Institut f\"ur Angewandte Mathematik,
Universit\"at Bonn
Endenicher Allee 60, 53115 Bonn, Germany
email: kurzke@iam.uni-bonn.de
|
|---|
Return to the EJDE web page
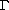 -convergence for Ginzburg-Landau
type functionals. We only assume that the
potential is continuous and positive definite close to one
circular well, but allow large zero sets inside the well.
We show that the relaxation of the assumptions does not change
the results to leading order unless the energy is very large.
-convergence for Ginzburg-Landau
type functionals. We only assume that the
potential is continuous and positive definite close to one
circular well, but allow large zero sets inside the well.
We show that the relaxation of the assumptions does not change
the results to leading order unless the energy is very large.
