In this article, we study the uniform asymptotic stability of the switched system
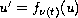 ,
,
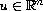 , where
, where
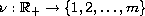 is an arbitrary
piecewise constant function.
We find criteria for the asymptotic stability of nonlinear
systems. In particular, for slow and homogeneous systems,
we prove that the asymptotic stability of each individual
equation
is an arbitrary
piecewise constant function.
We find criteria for the asymptotic stability of nonlinear
systems. In particular, for slow and homogeneous systems,
we prove that the asymptotic stability of each individual
equation
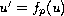 (
(
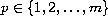 )
implies the uniform asymptotic stability of the system
(with respect to switched signals).
For linear switched systems (i.e.,
)
implies the uniform asymptotic stability of the system
(with respect to switched signals).
For linear switched systems (i.e.,
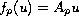 , where
, where
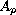 is a linear mapping acting on
is a linear mapping acting on
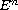 )
we establish the following
result: The linear switched system is uniformly asymptotically stable
if it does not admit nontrivial bounded full trajectories and
at least one of the equations
)
we establish the following
result: The linear switched system is uniformly asymptotically stable
if it does not admit nontrivial bounded full trajectories and
at least one of the equations
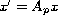 is asymptotically stable.
We study this problem in the framework of linear non-autonomous
dynamical systems (cocyles).
is asymptotically stable.
We study this problem in the framework of linear non-autonomous
dynamical systems (cocyles).

