Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 174, pp. 1-10.
Necessary and sufficient conditions for the oscillation
a third-order differential equation
Pitambar Das, Jitendra Kumar Pati
Abstract:
We show that under certain restrictions the following three conditions
are equivalent: The equation
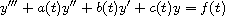
is oscillatory. The equation
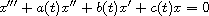
is oscillatory. The second-order Riccati equation
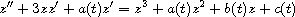
does not admit a non-oscillatory solution that is eventually
positive.
Furthermore, we obtain sufficient conditions for the above statements to
hold, in terms of the coefficients.
These conditions are sharp in the sense that they are both
necessary and sufficient when the coefficients
 are
constant.
are
constant.
Submitted April 13, 2010. Published December 6, 2010.
Math Subject Classifications: 34C10, 34C15.
Key Words: Oscillation; non-oscillation; third order differential equations.
Show me the PDF file (224 KB),
TEX file, and other files for this article.
 |
Pitambar Das
Department of Mathematics,
Indira Gandhi Institute of Technology
Sarang-759146, Talcher, Orissa, India
email: pdasigit@in.com
|
|---|
 |
Jitendra Kumar Pati
Department of Mathematics,
Indira Gandhi Institute of Technology
Sarang-759146, Talcher, Orissa, India
email: jkpati2007@yahoo.com
|
|---|
Return to the EJDE web page
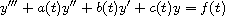
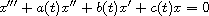
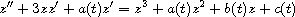
 are
constant.
are
constant.

