Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 162, pp. 1-23.
Existence of solutions to indefinite quasilinear
elliptic problems of p-q-Laplacian type
Nikolaos E. Sidiropoulos
Abstract:
We study the indefinite quasilinear elliptic problem
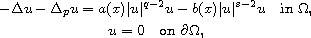
where
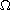 is a bounded domain in
is a bounded domain in
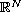 ,
,
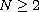 ,
with a sufficiently smooth boundary,
,
with a sufficiently smooth boundary,
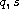 are subcritical exponents,
are subcritical exponents,
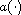 changes
sign and
changes
sign and
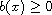 a.e. in
a.e. in
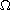 .
Our proofs are variational
in character and are based either on the fibering method or the
mountain pass theorem.
.
Our proofs are variational
in character and are based either on the fibering method or the
mountain pass theorem.
Submitted July 7, 2010. Published November 12, 2010.
Math Subject Classifications: 35J60, 35J62, 35J92.
Key Words: Indefinite quasilinear elliptic problems;
subcritical nonlinearities; p-Laplacian;
p-q-Laplacian; fibering method; mountain pass theorem.
Show me the PDF file (337 KB),
TEX file, and other files for this article.
 |
Nikolaos E. Sidiropoulos
Department of Sciences, Technical University of Crete
73100 Chania, Greece
email: niksidirop@gmail.com
|
|---|
Return to the EJDE web page
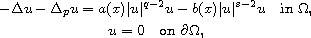
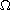 is a bounded domain in
is a bounded domain in
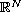 ,
,
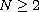 ,
with a sufficiently smooth boundary,
,
with a sufficiently smooth boundary,
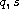 are subcritical exponents,
are subcritical exponents,
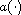 changes
sign and
changes
sign and
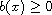 a.e. in
a.e. in
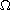 .
Our proofs are variational
in character and are based either on the fibering method or the
mountain pass theorem.
.
Our proofs are variational
in character and are based either on the fibering method or the
mountain pass theorem.
