We establish regularity conditions for the 3D Navier-Stokes equation via two components of the vorticity vector. It is known that if a Leray-Hopf weak solution
 satisfies
satisfies
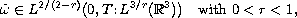
where
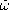 form the two components of the vorticity,
form the two components of the vorticity,
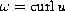 , then
, then
 becomes the classical
solution on
becomes the classical
solution on
![$(0,T]$](gifs/ae.gif) (see [5]).
We prove the regularity
of Leray-Hopf weak solution
(see [5]).
We prove the regularity
of Leray-Hopf weak solution
 under each of the following
two (weaker) conditions:
under each of the following
two (weaker) conditions:
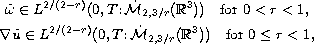
where
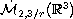 is the
Morrey-Campanato space.
Since
is the
Morrey-Campanato space.
Since
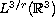 is a proper subspace of
is a proper subspace of
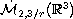 , our regularity
criterion improves the results in Chae-Choe [5].
, our regularity
criterion improves the results in Chae-Choe [5].