Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 15, pp. 1-10.
Entire solutions for a class of p-Laplace equations in R^2
Zheng Zhou
Abstract:
We study the entire solutions of
the p-Laplace equation
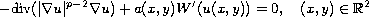
where a(x,y) is a periodic in x and y, positive function. Here
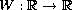 is a two well potential. Via variational
methods, we show that there is layered solution which is heteroclinic
in x and periodic in y direction.
is a two well potential. Via variational
methods, we show that there is layered solution which is heteroclinic
in x and periodic in y direction.
Submitted September 15, 2009. Published January 21, 2010.
Math Subject Classifications: 35J60, 35B05, 35B40.
Key Words: Entire solution; p-Laplace Allen-Cahn equation;
Variational methods.
Show me the PDF file (230 KB),
TEX file, and other files for this article.
 |
Zheng Zhou
College of Mathematics and Econometrics
Hunan University, Changsha, China
email: zzzzhhhoou@yahoo.com.cn
|
|---|
Return to the EJDE web page
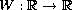 is a two well potential. Via variational
methods, we show that there is layered solution which is heteroclinic
in x and periodic in y direction.
is a two well potential. Via variational
methods, we show that there is layered solution which is heteroclinic
in x and periodic in y direction.
