In this article, we prove the existence and upper semicontinuity of compact global attractors for the flow of the equation
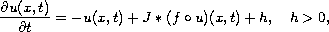
in
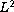 weighted spaces.
weighted spaces.
Severino Horacio da Silva
Abstract:
In this article, we prove the existence and upper semicontinuity of
compact global attractors for the flow of the equation
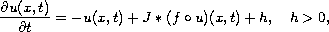
in
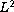 weighted spaces.
weighted spaces.
Submitted March 16, 2010. Published September 27, 2010.
Math Subject Classifications: 45J05, 45M05, 34D45.
Key Words: Well-posedness; global attractor;
upper semicontinuity of attractors.
Show me the PDF file (150 KB), TEX file, and other files for this article.
 |
Severino Horácio da Silva Unidade Acadêmica de Matemática e Estatística UAME/CCT/UFCG Rua Aprígio Veloso, 882, Bairro Universitário CEP 58429-900 Campina Grande-PB, Brasil email: horacio@dme.ufcg.edu.br |
|---|
Return to the EJDE web page