Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 133, pp. 1-10.
Spectral concentration in Sturm-Liouville equations with large
negative potential
Bernard J. Harris, Jeffrey C. Kallenbach
Abstract:
We consider the spectral function,
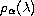 ,
associated with the linear second-order question
,
associated with the linear second-order question
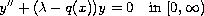
and the initial condition
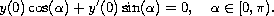
in the case where
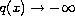 as
as
 .
We obtain a representation of
.
We obtain a representation of
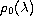 as a convergent
series for
as a convergent
series for
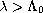 where
where
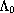 is computable,
and a bound for the points of spectral concentration.
is computable,
and a bound for the points of spectral concentration.
Submitted August 27, 2009. Published September 14, 2010.
Math Subject Classifications: 34L05, 34L20.
Key Words: Spectral theory; Schrodinger equation.
Show me the PDF file (219 KB),
TEX file, and other files for this article.
 |
Bernard J. Harris
Department of Mathematical Sciences
Northern Illinois University
DeKalb, IL 60115, USA
email: harris@math.niu.edu
|
|---|
 |
Jeffrey C. Kallenbach
Department of Mathematical Sciences
Siena Heights University
Adrian, MI 49221, USA
email: jkallenb@siennaheights.edu
|
|---|
Return to the EJDE web page
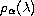 ,
associated with the linear second-order question
,
associated with the linear second-order question
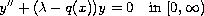
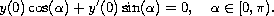
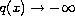 as
as
 .
We obtain a representation of
.
We obtain a representation of
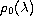 as a convergent
series for
as a convergent
series for
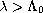 where
where
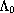 is computable,
and a bound for the points of spectral concentration.
is computable,
and a bound for the points of spectral concentration.

