Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 130, pp. 1-11.
Constant invariant solutions of the Poincare center-focus problem
Gary R. Nicklason
Abstrac:
We consider the classical Poincare problem
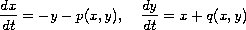
where
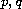 are homogeneous polynomials of degree
are homogeneous polynomials of degree
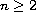 .
Associated with this system is an Abel differential equation
.
Associated with this system is an Abel differential equation
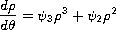
in which the coefficients are trigonometric polynomials.
We investigate two separate conditions which produce a constant
first absolute invariant of this equation. One of these conditions
leads to a new class of integrable, center conditions for the
Poincare problem if
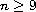 is an odd integer.
We also show that both classes of solutions produce polynomial
solutions to the problem.
is an odd integer.
We also show that both classes of solutions produce polynomial
solutions to the problem.
Submitted June 7, 2010. Published September 14, 2010.
Math Subject Classifications: 34A05, 34C25.
Key Words: Center-focus problem; Abel differential equation;
constant invariant; symmetric centers.
Show me the PDF file (226 KB),
TEX file, and other files for this article.
 |
Gary R. Nicklason
Mathematics, Physics and Geology
Cape Breton University
Sydney, Nova Scotia, Canada B1P 6L2
email: gary_nicklason@capebretonu.ca
|
|---|
Return to the EJDE web page
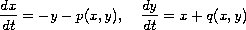
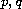 are homogeneous polynomials of degree
are homogeneous polynomials of degree
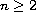 .
Associated with this system is an Abel differential equation
.
Associated with this system is an Abel differential equation
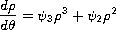
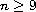 is an odd integer.
We also show that both classes of solutions produce polynomial
solutions to the problem.
is an odd integer.
We also show that both classes of solutions produce polynomial
solutions to the problem.
