Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 127, pp. 1-8.
Existence of periodic solutions for neutral nonlinear
differential equations with variable delay
Deham Hafsia, Djoudi Ahcene
Abstract:
We use a variation of Krasnoselskii fixed point theorem
introduced by Burton to show that the nonlinear neutral differential
equation
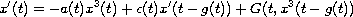
has a periodic solution. Since this equation is nonlinear,
the variation of parameters can not be applied directly;
we add and subtract a linear term to transform the
differential into an equivalent integral equation suitable
for applying a fixed point theorem. Our result is illustrated
with an example.
Submitted April 15, 2010. Published September 7, 2010.
Math Subject Classifications: 34K20, 45J05, 45D05.
Key Words: Periodic solution; nonlinear neutral differential equation;
large contraction, integral equation.
Show me the PDF file (199 KB),
TEX file, and other files for this article.
 |
Deham Hafsia
Department of Mathematics, Faculty of Sciences
University of Annaba, P.O. Box 12 Annaba, Algeria
email: deh_71@yahoo.fr
|
|---|
| |
Djoudi Ahcéne
Department of Mathematics, Faculty of Sciences
University of Annaba, P.O. Box 12 Annaba, Algeria
email: adjoudi@yahoo.com
|
|---|
Return to the EJDE web page