Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 12, pp. 1-12.
Existence of solutions to singular elliptic equations with
convection terms via the Galerkin method
Claudianor O. Alves, Paulo C. Carriao, Luiz F. O. Faria
Abstract:
In this article, we use the Galerkin method to show the existence
of solutions for the following elliptic equation with convection term
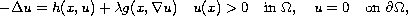
where
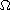 is a bounded domain,
is a bounded domain,
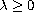 is a parameter,
is a parameter,
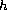 has sublinear and singular terms, and
has sublinear and singular terms, and
 is a continuous function.
is a continuous function.
Submitted June 22, 2009. Published June 18, 2010.
Math Subject Classifications: 35J60, 35B25.
Key Words: Singular elliptic equation; convection term; Galerkin method.
Show me the PDF file (248 KB),
TEX file, and other files for this article.
 |
Claudianor O. Alves
Unidade Acadêmica de Matemática e Estatística
Universidade Federal de Campina Grande
58109-970, Campina Grande - PB, Brazil
email: coalves@dme.ufcg.edu.br
|
|---|
 |
Paulo C. Carrião
Departamento de Matemática - Instituto de Ciências Exatas
Universidade Federal de Minas Gerais
30161-970, Belo Horizonte - MG, Brazil
email: carrion@mat.ufmg.br
|
|---|
 |
Luiz F. O. Faria
Departamento de Matemática - Instituto de Ciências Exatas
Universidade Federal de Juiz de Fora
30161-970, Juiz de Fora - MG, Brazil
email: luiz.faria@ufjf.edu.br
|
|---|
Return to the EJDE web page
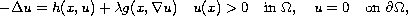
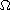 is a bounded domain,
is a bounded domain,
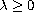 is a parameter,
is a parameter,
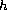 has sublinear and singular terms, and
has sublinear and singular terms, and
 is a continuous function.
is a continuous function.


