Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 116, pp. 1-14.
Asymptotic behavior of ground state solution for Henon type systems
Ying Wang, Jianfu Yang
Abstract:
In this article, we investigate the asymptotic behavior of
positive ground state solutions, as
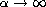 ,
for the following Henon type system
,
for the following Henon type system
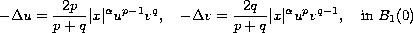
with zero boundary condition, where
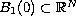 (
(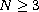 )
is the unit ball centered at the origin,
)
is the unit ball centered at the origin,
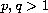 ,
,
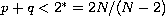 .
We show that both components of the ground solution pair
.
We show that both components of the ground solution pair
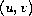 concentrate on the same point on the boundary
concentrate on the same point on the boundary
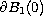 as
as
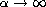 .
.
Submitted July 14, 2010. Published August 20, 2010.
Math Subject Classifications: 35J50, 35J57, 35J47.
Key Words: Asymptotic behavior; Henon systems; ground state solution
Show me the PDF file (256 KB),
TEX file, and other files for this article.
Ying Wang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: yingwang00@126.com
|
Jianfu Yang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
Return to the EJDE web page
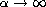 ,
for the following Henon type system
,
for the following Henon type system
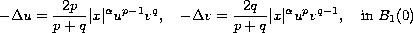
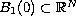 (
(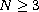 )
is the unit ball centered at the origin,
)
is the unit ball centered at the origin,
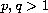 ,
,
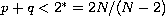 .
We show that both components of the ground solution pair
.
We show that both components of the ground solution pair
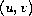 concentrate on the same point on the boundary
concentrate on the same point on the boundary
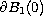 as
as
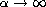 .
.