In this article, the author studies the regularity of 3D generalized Navier-Stokes (GNS) equations with fractional dissipative terms
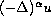 .
It is proved that if
.
It is proved that if
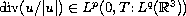 with
with
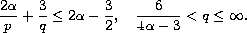
then any smooth on GNS in
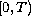 remains smooth on
remains smooth on
![$[0, T]$](gifs/ae.gif) .
.
Yuwen Luo
Abstract:
In this article, the author studies the regularity of 3D generalized
Navier-Stokes (GNS) equations with fractional dissipative terms
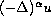 .
It is proved that if
.
It is proved that if
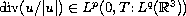 with
with
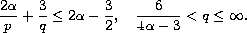
then any smooth on GNS in
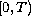 remains smooth on
remains smooth on
![$[0, T]$](gifs/ae.gif) .
.
Submitted April 8, 2010. Published August 2, 2010.
Math Subject Classifications: 35D10, 35Q35, 76D03.
Key Words: Generalized Navier-Stokes equation;
regularity; Serrin criteria.
Show me the PDF file (178 KB), TEX file, and other files for this article.
 |
Yuwen Luo School of Mathematics and Statistics Chongqing University of Technology Chongqing 400050, China email: petitevin@gmail.com |
|---|
Return to the EJDE web page