Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 09, pp. 1-12.
On the penalized obstacle problem in the unit half ball
Erik Lindgren
Abstract:
We study the penalized obstacle problem in the unit half ball,
i.e. an approximation of the obstacle problem in the
unit half ball. The main result states that when the approximation
parameter is small enough and when certain level sets are sufficiently
close to the hyperplane
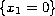 , then these level sets are
uniformly
, then these level sets are
uniformly
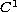 regular graphs. As a by-product, we also recover some
regularity of the free boundary for the limiting problem, i.e., for
the obstacle problem.
regular graphs. As a by-product, we also recover some
regularity of the free boundary for the limiting problem, i.e., for
the obstacle problem.
Submitted September 21, 2009. Published January 16, 2010.
Math Subject Classifications: 35J70, 35J60, 35J85
Key Words: Obstacle problem; elliptic equation; regularity; penalization.
Show me the PDF file (250 KB),
TEX file, and other files for this article.
 |
Erik Lindgren
CERMICS - ENPC, 6 et 8 avenue Blaise Pascal
Cite Descartes Champs sur Marne
77455 Marne la Vallee Cedex 2 France
email: erik.lindgren@cermics.enpc.fr
|
|---|
Return to the EJDE web page
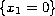 , then these level sets are
uniformly
, then these level sets are
uniformly
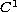 regular graphs. As a by-product, we also recover some
regularity of the free boundary for the limiting problem, i.e., for
the obstacle problem.
regular graphs. As a by-product, we also recover some
regularity of the free boundary for the limiting problem, i.e., for
the obstacle problem.
