Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 02, pp. 1-10.
Optimization in problems involving the p-Laplacian
Monica Marras
Abstract:
We minimize the energy integral
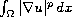 , where
, where
 is a bounded
positive function that varies in a class of rearrangements,
is a bounded
positive function that varies in a class of rearrangements,
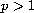 , and
, and
 is a solution of
is a solution of
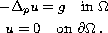
Also we maximize the first eigenvalue
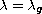 , where
, where
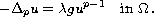
For both problems, we prove existence,
uniqueness, and representation of the optimizers.
Submitted November 2, 2009. Published January 5, 2010.
Math Subject Classifications: 35J25, 49K20, 47A75.
Key Words: p-Laplacian; energy integral; eigenvalues; rearrangements;
shape optimization
Show me the PDF file (219 KB),
TEX file, and other files for this article.
 |
Monica Marras
Dipartimento di Matematica e Informatica
Universitá di Cagliari
Via Ospedale 72, 09124 Cagliari, Italy
email: mmarras@unica.it
|
|---|
Return to the EJDE web page
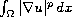 , where
, where
 is a bounded
positive function that varies in a class of rearrangements,
is a bounded
positive function that varies in a class of rearrangements,
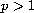 , and
, and
 is a solution of
is a solution of
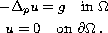
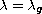 , where
, where