Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 82, pp. 1-9.
On the Cauchy-problem for generalized
Kadomtsev-Petviashvili-II equations
Axel Grunrock
Abstract:
The Cauchy-problem for the generalized
Kadomtsev-Petviashvili-II equation
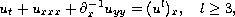
is shown to be locally well-posed in almost
critical anisotropic Sobolev spaces. The proof
combines local smoothing and maximal function
estimates as well as bilinear refinements of
Strichartz type inequalities via multilinear
interpolation in
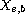 -spaces.
-spaces.
Submitted April 9, 2009. Published July 10, 2009.
Math Subject Classifications: 35Q53.
Key Words: Cauchy-problem; local well-posedness;
generalized KP-II equations.
Show me the PDF file (233 KB),
TEX file, and other files for this article.
Axel Grünrock
Rheinische Friedrich-Wilhelms-Universit&uaml;t Bonn,
Mathematisches Institut
Beringstrase 1, 53115 Bonn, Germany
email: gruenroc@math.uni-bonn.de |
|
Return to the EJDE web page
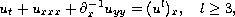
 -spaces.
-spaces.