Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 81, pp. 1-10.
Existence of weak solutions for nonlinear systems involving
several p-Laplacian operators
Salah A. Khafagy, Hassan M. Serag
Abstract:
In this article, we study nonlinear systems involving several p-Laplacian
operators with variable coefficients. We consider the system

where
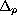 denotes the p-Laplacian defined by
denotes the p-Laplacian defined by
![$\Delta_{p}u\equiv \hbox{div} [|\nabla u|^{p-2}\nabla u]$](gifs/ac.gif) with
with
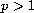 ,
,
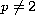 ;
;
 ;
;
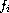 are given functions;
and the coefficients
are given functions;
and the coefficients
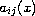 (
(
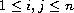 )
are bounded
smooth positive functions. We prove the existence of
weak solutions defined on bounded and unbounded domains
using the theory of nonlinear monotone operators.
)
are bounded
smooth positive functions. We prove the existence of
weak solutions defined on bounded and unbounded domains
using the theory of nonlinear monotone operators.
Submitted December 9, 2008. Published July 10, 2009.
Math Subject Classifications: 74H20, 35J65.
Key Words: Existence of weak solution; nonlinear system, p-Laplacian.
Show me the PDF file (227 KB),
TEX file, and other files for this article.
 |
Salah A. Khafagy
Mathematics Department, Faculty of Science
Al-Azhar University, Nasr City 11884, Cairo, Egypt
email: el_gharieb@hotmail.com
|
|---|
 |
Hassan M. Serag
Mathematics Department, Faculty of Science
Al-Azhar University, Nasr City 11884, Cairo, Egypt
email: serraghm@yahoo.com
|
|---|
Return to the EJDE web page

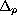 denotes the p-Laplacian defined by
denotes the p-Laplacian defined by
![$\Delta_{p}u\equiv \hbox{div} [|\nabla u|^{p-2}\nabla u]$](gifs/ac.gif) with
with
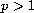 ,
,
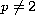 ;
;
 ;
;
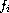 are given functions;
and the coefficients
are given functions;
and the coefficients
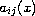 (
(
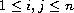 )
are bounded
smooth positive functions. We prove the existence of
weak solutions defined on bounded and unbounded domains
using the theory of nonlinear monotone operators.
)
are bounded
smooth positive functions. We prove the existence of
weak solutions defined on bounded and unbounded domains
using the theory of nonlinear monotone operators.

